Working with Transformation Matrices in Swift
As part of some recent work, I was working on implementing applying transforms to 3D objects in a Swift app. I was having a really difficult time gaining an intuitive understanding of how the matrices behaved.
I had Claude help me generate a test app to visualize how modifying position, scale, and rotation values would affect the resulting matrices being used to modify the blue 3D cube.
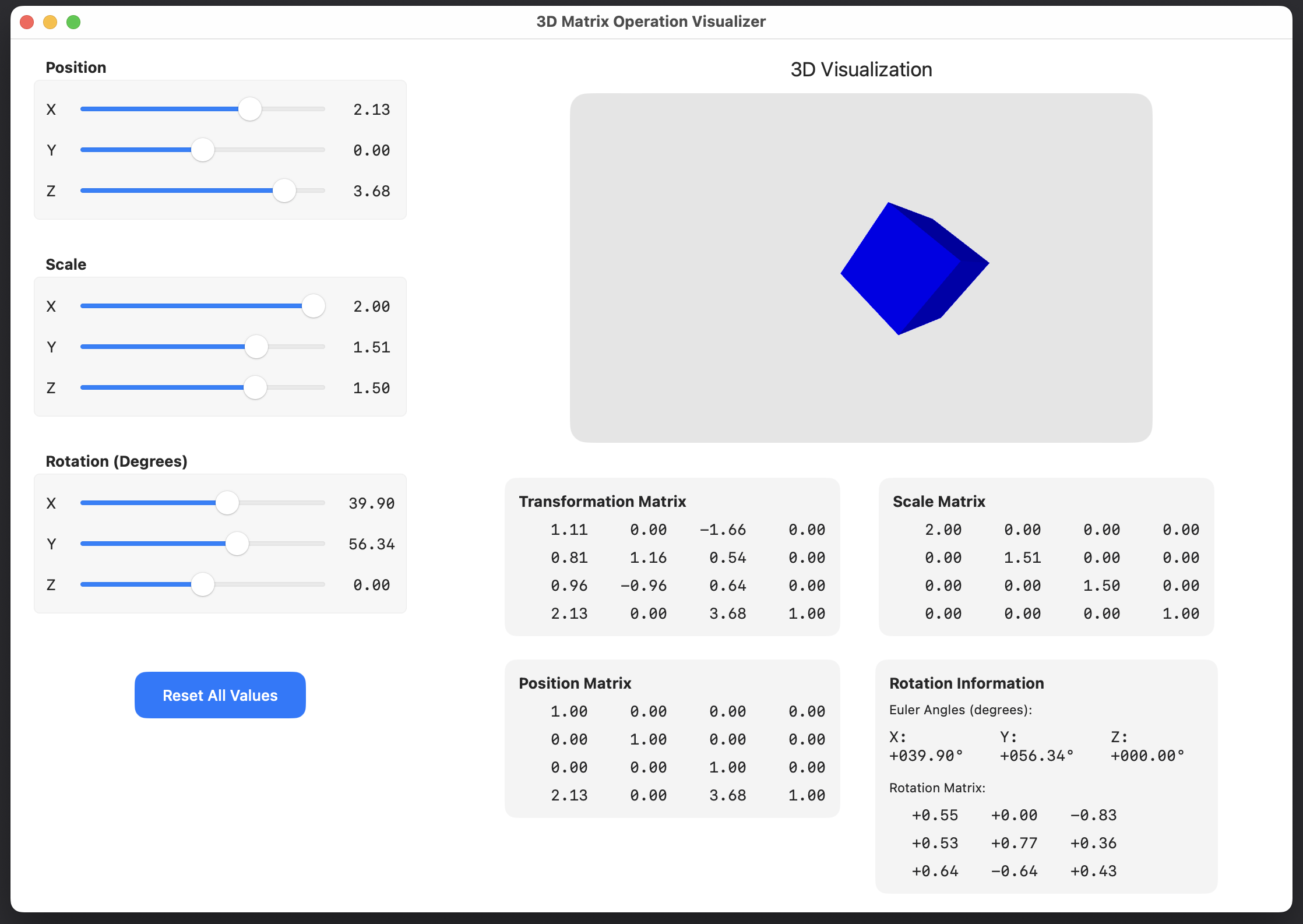
This helped me to gain a better understanding of how the matrices behaved. I had previously assumed that there would be a one-to-one mapping
The code for this app can be found here: narner/3D-Matrix-Operation-Visualizer: Real-time 3D object transformation demo for Swift
Matrix Representation
A transformation matrix in 3D is typically a 4x4 matrix, which allows for the representation of both linear transformations (like rotation and scaling) and translations (movement in space). The general form of a 4x4 transformation matrix is:
| | | m11 | m12 | m13 | m14 | | |
| | | m21 | m22 | m23 | m24 | | |
| | | m31 | m32 | m33 | m34 | | |
| | | 0 | 0 | 0 | 1 | | |
The top-left 3x3 submatrix (m11 to m33) represents the rotation and scaling of the object.
| | | m11 | m12 | m13 | m14 | | |
| | | m21 | m22 | m23 | m24 | | |
| | | m31 | m32 | m33 | m34 | | |
| | | 0 | 0 | 0 | 1 | | |
The fourth column (m14, m24, m34) represents the translation (position) of the object in 3D space.
| | | m11 | m12 | m13 | m14 | | |
| | | m21 | m22 | m23 | m24 | | |
| | | m31 | m32 | m33 | m34 | | |
| | | 0 | 0 | 0 | 1 | | |
The bottom row is typically [0, 0, 0, 1], which is used to maintain the properties of homogeneous coordinates.
| | | m11 | m12 | m13 | m14 | | |
| | | m21 | m22 | m23 | m24 | | |
| | | m31 | m32 | m33 | m34 | | |
| | | 0 | 0 | 0 | 1 | | |
We’ll look at ways to extract specific properties of the transformation matrix from code in simd_float4x4+Extension.swift.
Transformation Types
Translation: These are used to move an object from one location to another, and can be represented as:
| | | m11 | m12 | m13 | m14 | | |
| | | m21 | m22 | m23 | m24 | | |
| | | m31 | m32 | m33 | m34 | | |
| | | tx | ty | tz | 1 | | |
Where (tx, ty, tz) are the translation distances along the x, y, and z axes. This can be represented in Swift like so:
var position: SIMD3<Float> {
.init(columns.3.x, columns.3.y, columns.3.z)
}
Scaling: This changes the size of an object. The scaling matrix is defined as:
| | | sx | sy | sz | m14 | | |
| | | m21 | m22 | m23 | m24 | | |
| | | m31 | m32 | m33 | m34 | | |
| | | tx | ty | tz | 1 | | |
Where (sx, sy, sz) are the scaling factors along the respective axes.
var scale: SIMD3<Float> {
.init(
simd_length(SIMD3<Float>(columns.0.x, columns.0.y, columns.0.z)),
simd_length(SIMD3<Float>(columns.1.x, columns.1.y, columns.1.z)),
simd_length(SIMD3<Float>(columns.2.x, columns.2.y, columns.2.z))
)
}
Rotation: The rotation matrices are used to rotate an object around the X, Y, and Z axes; and can be represented as:
Rotation around X-axis:
| | | 1 | 0 | 1 | 0 | | |
| | | 0 | cos(θ) | -sin(θ) | 0 | | |
| | | 0 | sin(θ) | cos(θ) | 0 | | |
| | | 0 | 0 | 0 | 1 | | |
Rotation around Y-axis:
| | | cos(θ) | 0 | sin(θ) | 0 | | |
| | | 0 | 1 | 0 | 0 | | |
| | | -sin(θ) | 0 | cos(θ) | 0 | | |
| | | 0 | 0 | 0 | 1 | | |
Rotation around Z-axis:
| | | cos(θ) | -sin(θ) | 0 | 0 | | |
| | | sin(θ) | cos(θ) | 0 | 0 | | |
| | | 0 | 0 | 1 | 0 | | |
| | | 0 | 0 | 0 | 1 | | |
This can be represented in Swift like so:
var rotationMatrix: simd_float3x3 {
let scale = self.scale
return simd_float3x3(
SIMD3<Float>(columns.0.x, columns.0.y, columns.0.z) / scale.x,
SIMD3<Float>(columns.1.x, columns.1.y, columns.1.z) / scale.y,
SIMD3<Float>(columns.2.x, columns.2.y, columns.2.z) / scale.z
)
}
Matrix Creation
There are a couple of ways to create Transformation Matrix from scratch. The init function below takes a SIMD3<Float> of Euler angles as input, and constructs a matrix out of them.
init(rotationZYX eulerAngles: SIMD3<Float>) {
// Convert degrees to radians
let radiansX = eulerAngles.x * Float.pi / 180
let radiansY = eulerAngles.y * Float.pi / 180
let radiansZ = eulerAngles.z * Float.pi / 180
let cx = cos(radiansX), sx = sin(radiansX)
let cy = cos(radiansY), sy = sin(radiansY)
let cz = cos(radiansZ), sz = sin(radiansZ)
let rotationMatrix = simd_float3x3(
SIMD3<Float>(cy * cz, cy * sz, -sy),
SIMD3<Float>(sx * sy * cz - cx * sz, sx * sy * sz + cx * cz, sx * cy),
SIMD3<Float>(cx * sy * cz + sx * sz, cx * sy * sz - sx * cz, cx * cy)
)
self.init(rotationMatrix)
}
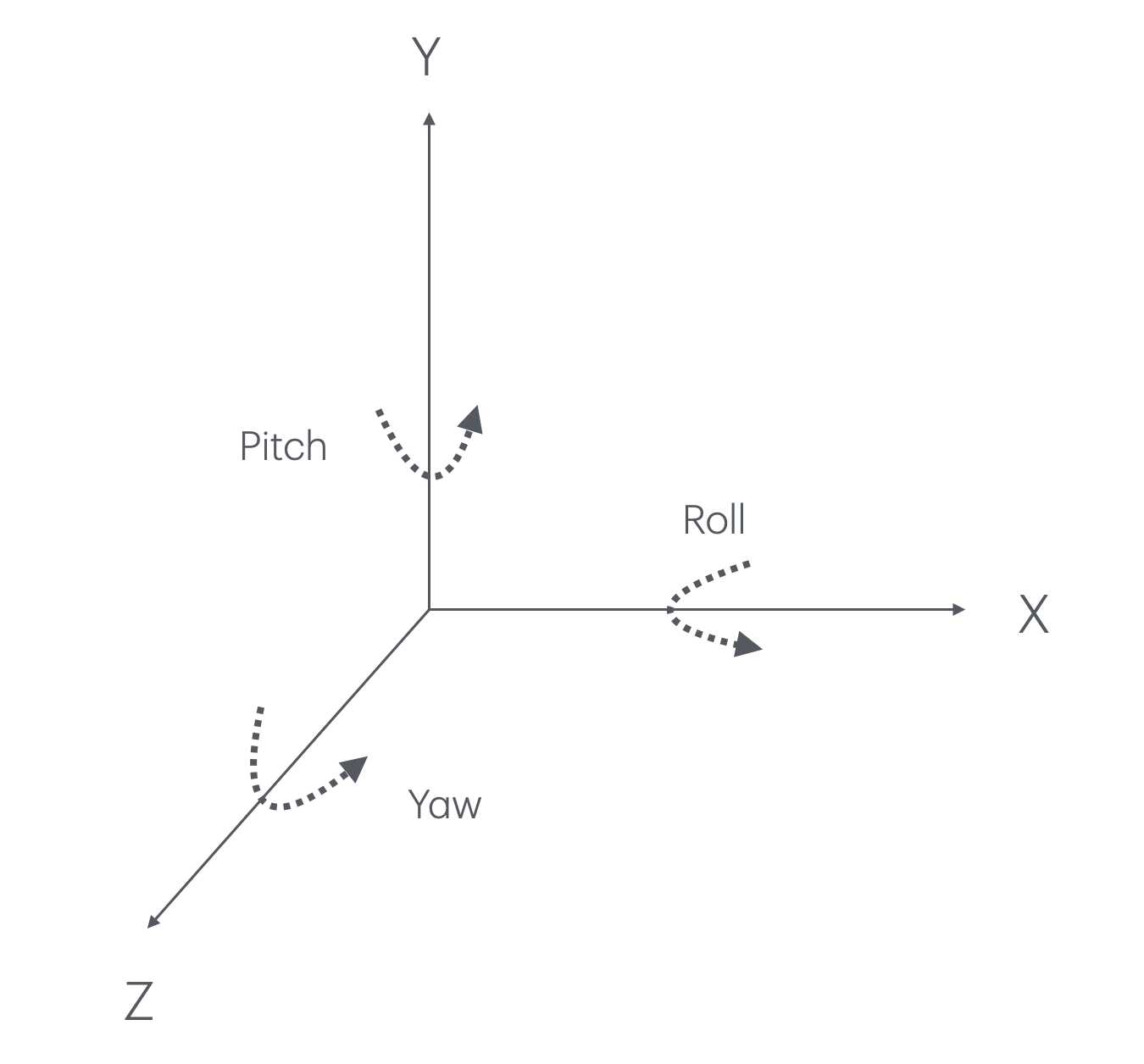
There are a couple of parts here worth looking at. First are Euler Angles. Euler Angles represent 3 different angles that describe rotation of an object around an axis. These angles are known as:
X-Axis (Roll)
Y-Axis (Pitch)
Z-Axis (Yaw)
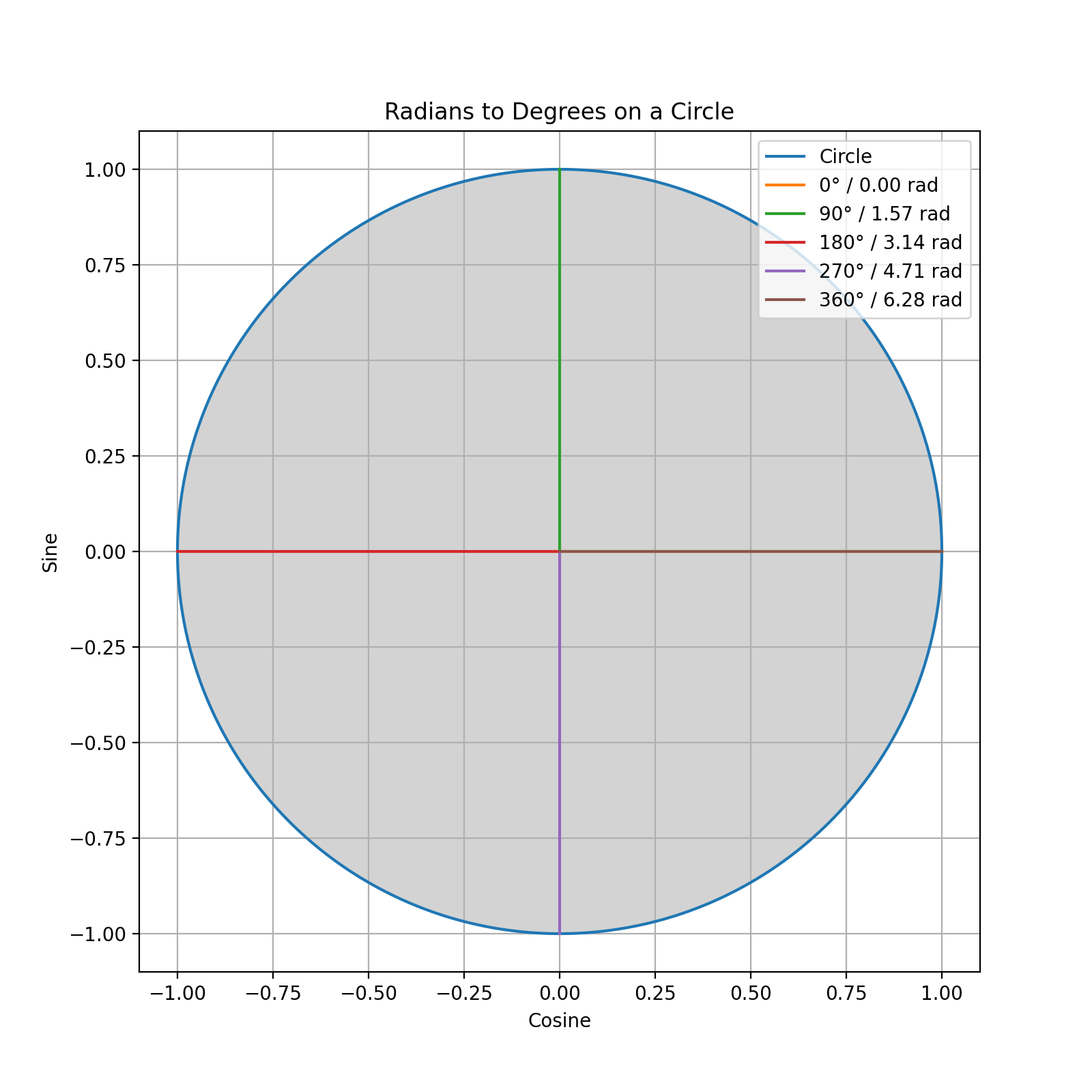
The second thing is the conversion from Radians to Degrees. A Degree is 1/360th of a full rotation around a circle. A radian is the angle formed when the arc length equals the radius of a circle. One full circle is about 6.28 (2π) radians.
You could construct the matrix directly from radians, however, degrees are much more common in user-facing applications for the reason that they are easier to reason about than radians.
Additionally, converting the Euler angles to degrees prior to creating the transform matrix allows for a visually smoother experience.
You can see that here: the first video shows what it looks like when we adjust the rotation of the cube in radians, and the second when we adjust it in degrees.
Final Thoughts
Understanding transformation matrices is crucial for Swift developers working in 3D graphics, games, or AR. By breaking down the 4x4 matrix components and visualizing their effects, we can understand how modifying transformation matrices can affect the scaling, position, and rotation of 3D objects.

